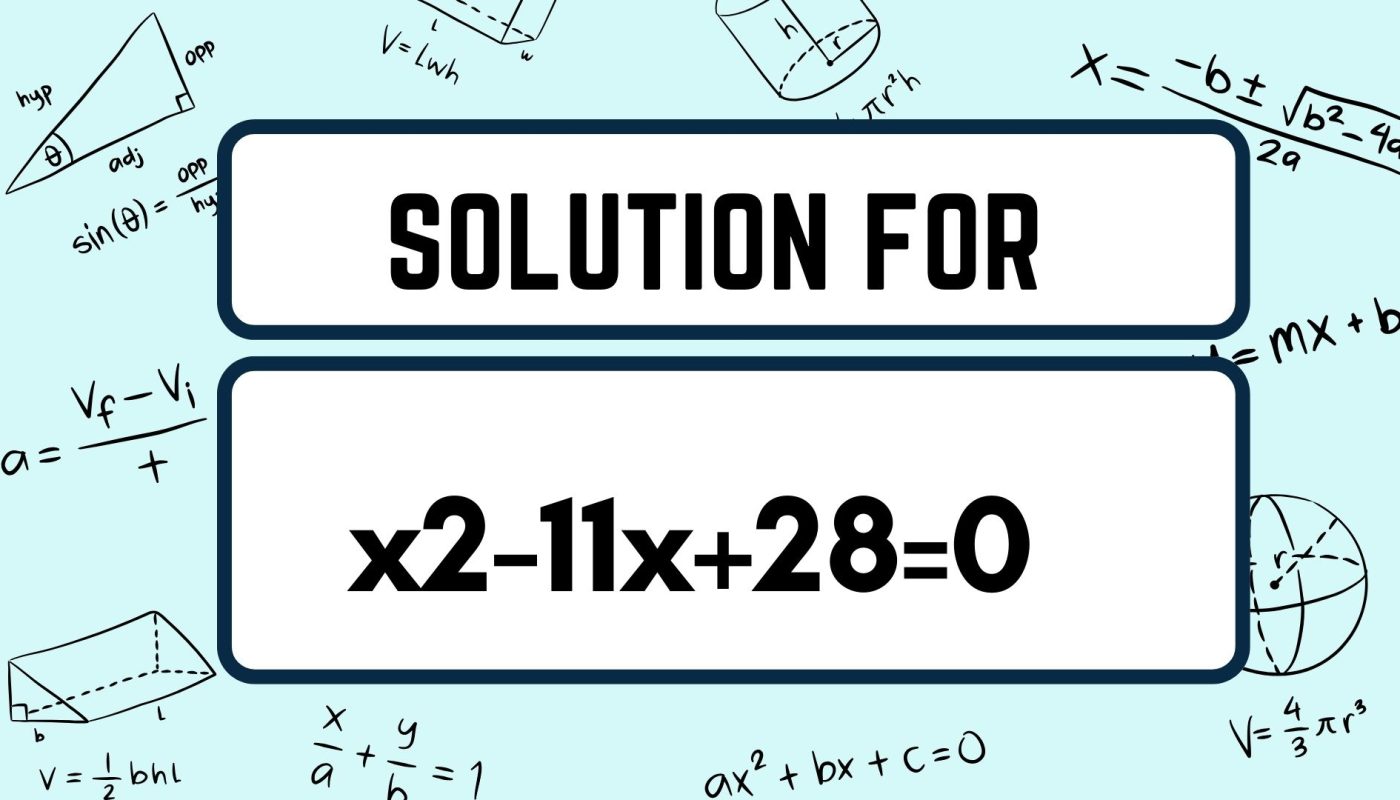Solve – x2-11x+28=0 | Methods and Solutions

In this article, we’ll delve into solving the specific quadratic equation ${}^{}$ and explore its implications. Quadratic equations are a fundamental part of algebra, representing a parabolic relationship in a variety of real-world scenarios. Let’s start with the solutions.

The Quadratic Equation – x2−11x+28=0

The general form of a quadratic equation is ax^2+bx+c=0. In our case, the equation ${}^{}$ can be identified with $$, $b=-11$, and $$.

Method 1: Factoring

The equation can be factored if we can find two numbers that multiply to 28 (the constant term) and add up to -11 (the coefficient of x). These numbers are -7 and -4. Therefore, the equation can be factored as:

${}^{}$

Setting each factor equal to zero gives us the solutions:

$$ $$

$$

Hence, the solutions are $\mathrm{}$ and $x=4$.

Method 2: Completing the Square

To solve by completing the square, rearrange the equation and complete the square on the left side:

1. Rearrange the equation: ${}^{}\mathrm{}$
2. Add the square of half the coefficient of x to both sides: ${\mathrm{x^2}}^{}-\mathrm{11x}+{\left(\frac{11}{2}\right)}^2=-28+{\left(\frac{11}{2}\right)}^2$ $\Rightarrow$  x^2$-11x+30.25=2.25$
   
3. Write the left side as a perfect square: $(x-5.5{)}^2=2.25$
   
4. Take the square root of both sides:  x$-5.5=\pm \sqrt{2.25}$
5. Solve for x:  $x=5.5\pm 1.5$

Thus, the solutions are $$ and $$.

Method 3: Quadratic Formula

The quadratic formula is $�=\frac{-b\pm \sqrt{b^2-4\mathrm{ac}}}{2a}$, where $$, $$, and $$ are coefficients from the quadratic equation $\mathrm{ax^}{2}^{}+\mathrm{bx}+c=0$. For our equation:

• $$
• $$
• $c=28$

Plugging these values into the formula:

$x=\frac{-(-11)\pm \sqrt{(-11{)}^2-4\cdot 1\cdot 28}}{2\cdot 1}$

$x=\frac{11\pm \sqrt{121-112}}{2}$

$x=\frac{11\pm \sqrt{9}}{2}$

$x=\frac{11\pm 3}{2}$

Therefore, the solutions are:

$x=\frac{11+3}{2}=7$

$x=\frac{11-3}{2}=4$

The solutions for ${}^{}$ are $$ and $$, irrespective of the method used

Also Read:

• Free Redeem Code Generator; Complete Knowledge
• Which Billionaires Own Bitcoin Today?
• Sad Shayari Punjabi

Graphical Interpretation

The graph of y=x2−11x+28 is a parabola opening upwards. The roots of the equation, $x=4$ and $$, represent the points where this parabola intersects the x-axis.

Conclusion

Solving quadratic equations like x2−11x+28=0 can be approached through various methods, each providing a unique perspective on the problem. The roots of this particular equation, 4 and 7, offer insights into the parabolic nature of quadratic relationships in mathematics and their applications.