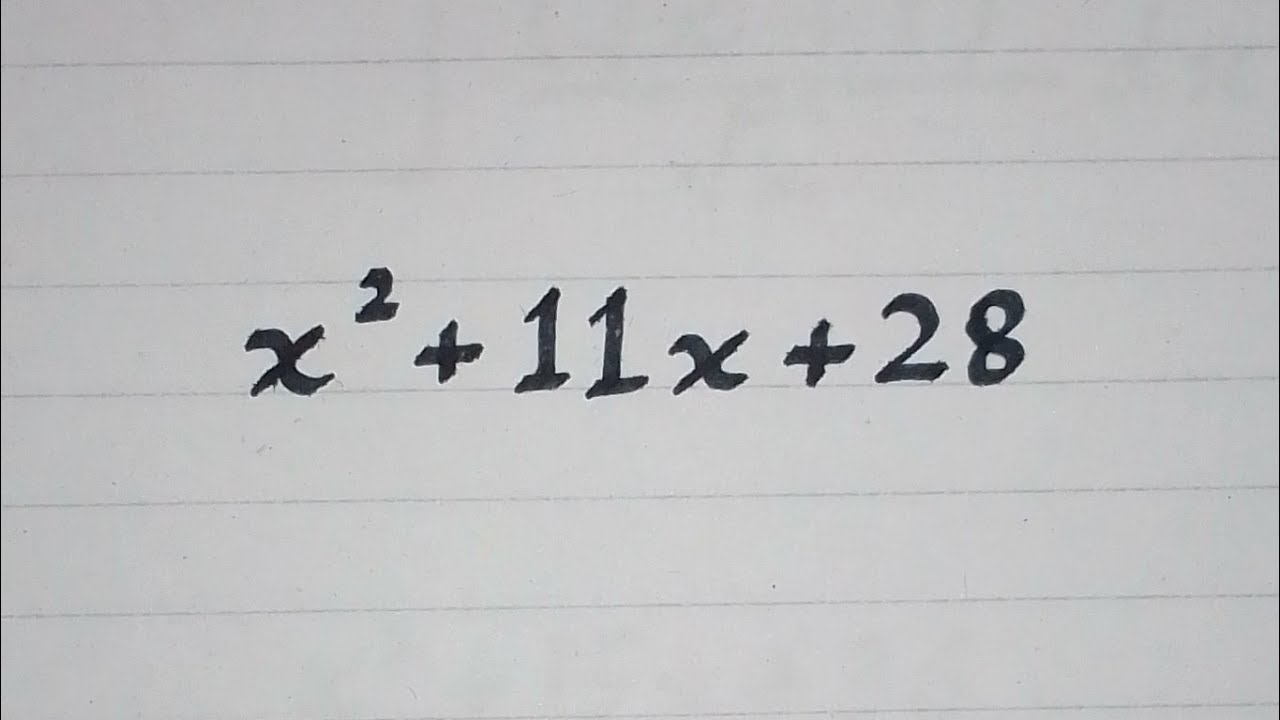Quadratic equations hold a prominent place in the realm of algebra, forming the cornerstone of polynomial functions with a degree of two. These equations, characterized by their standard form ax² + bx + c = 0, where ‘a’ is not equal to zero, are pivotal in various mathematical and scientific applications. The equation x2-11x+28=0 serves as a quintessential example of a quadratic equation, showcasing the intricate balance between its coefficients and the solutions it harbors. This article aims to delve into the methodologies for solving this equation, offering insights into the elegance of algebraic manipulation and the power of mathematical reasoning.
Detailed Understanding of the Equation x2-11x+28=0
At its core, the equation x2-11x+28=0 is a manifestation of the quadratic form, where:
- ‘a’, the coefficient of x², equals 1,
- ‘b’, the coefficient of x, is -11, and
- ‘c’, the constant term, stands at 28.
This equation, seemingly simple, encapsulates the challenge of finding the values of x that satisfy the equation, known as the roots of the equation.
Comprehensive Methods of Solving Quadratic Equations
To unravel the mystery of the quadratic equation, several methods stand at our disposal, each with its unique approach and insights. Let’s explore these methods in detail.
1. Factoring Method
Factoring is a technique that leans on the algebraic property that if the product of two expressions equals zero, then at least one of the expressions must be zero. This method involves decomposing the quadratic equation into a product of two binomials.
Step-by-Step Factoring:
For the equation at hand, x2-11x+28=0, the goal is to identify two numbers that, when multiplied, give 28 (the constant ‘c’) and, when added, result in -11 (the coefficient ‘b’).
- First, we split the middle term, -11x, into two terms that fulfill these conditions. After some deliberation, we find that -7x and -4x fit the criteria.
- Thus, we rewrite the equation as x² – 7x – 4x + 28 = 0.
- Next, we group the terms: (x² – 7x) – (4x – 28) = 0.
- Factoring out the common factors from each group, we get x(x – 7) – 4(x – 7) = 0.
- Recognizing that both groups contain the common factor (x – 7), we factor this out, resulting in (x – 7)(x – 4) = 0.
Hence, the roots of the equation are x = 7 and x = 4, as setting either factor to zero yields these solutions.
2. Completing the Square
Completing the square is a method that transforms the quadratic equation into a perfect square trinomial, thereby simplifying the process of finding the roots.
Detailed Steps for Completing the Square:
To apply this method to x² – 11x + 28 = 0, follow these steps:
- First, we ensure the coefficient of x² is 1. In this case, it already is.
- Then, we transpose the constant term to the other side, getting x2-11x+28=0.
- The next step involves adding the square of half the coefficient of x to both sides of the equation to form a perfect square on the left side. The coefficient of x is -11, so half of this is -11/2, and its square is (11/2)².
- Adding (11/2)² to both sides gives us (x – 11/2)² = 9/4.
- Taking the square root of both sides and solving for x yields x = 11/2 ± 3/2.
This results in the roots x = 7 and x = 4, identical to those found by factoring.
3. Quadratic Formula
The quadratic formula provides a universal solution to any quadratic equation, derived from the process of completing the square. It is represented as x = [-b ± √(b² – 4ac)] / (2a).
Applying the Quadratic Formula:
Applying this formula to our equation, where a = 1, b = -11, and c = 28:
- Plugging in these values gives us x = [11 ± √((-11)² – 4(1)(28))] / (2(1)).
- Simplifying under the square root, we find x = [11 ± √(121 – 112)] / 2.
- This simplifies further to x = [11 ± √9] / 2, resulting in x = 7 or x = 4.
Also read:
Conclusion
The exploration of the quadratic equation x2-11x+28=0 through the lenses of factoring, completing the square, and the quadratic formula not only elucidates the mathematical elegance inherent in solving such equations but also underscores the versatility and depth of algebra. Each method, with its unique perspective, converges to the same roots, x = 7 and x = 4, showcasing the interconnectedness of mathematical concepts. As we journey through these methodologies, we gain not just solutions to an equation but a deeper appreciation for the beauty and coherence of mathematics.